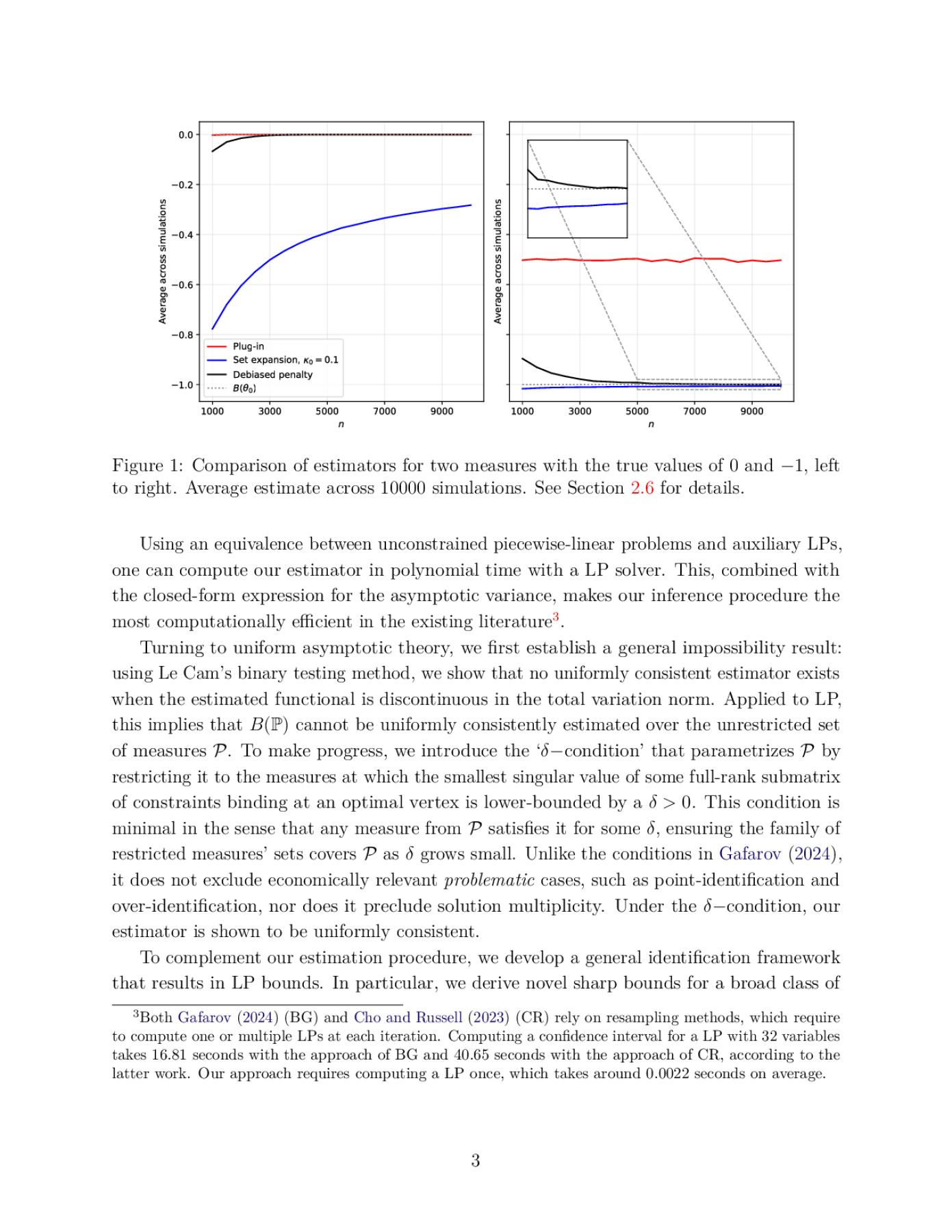
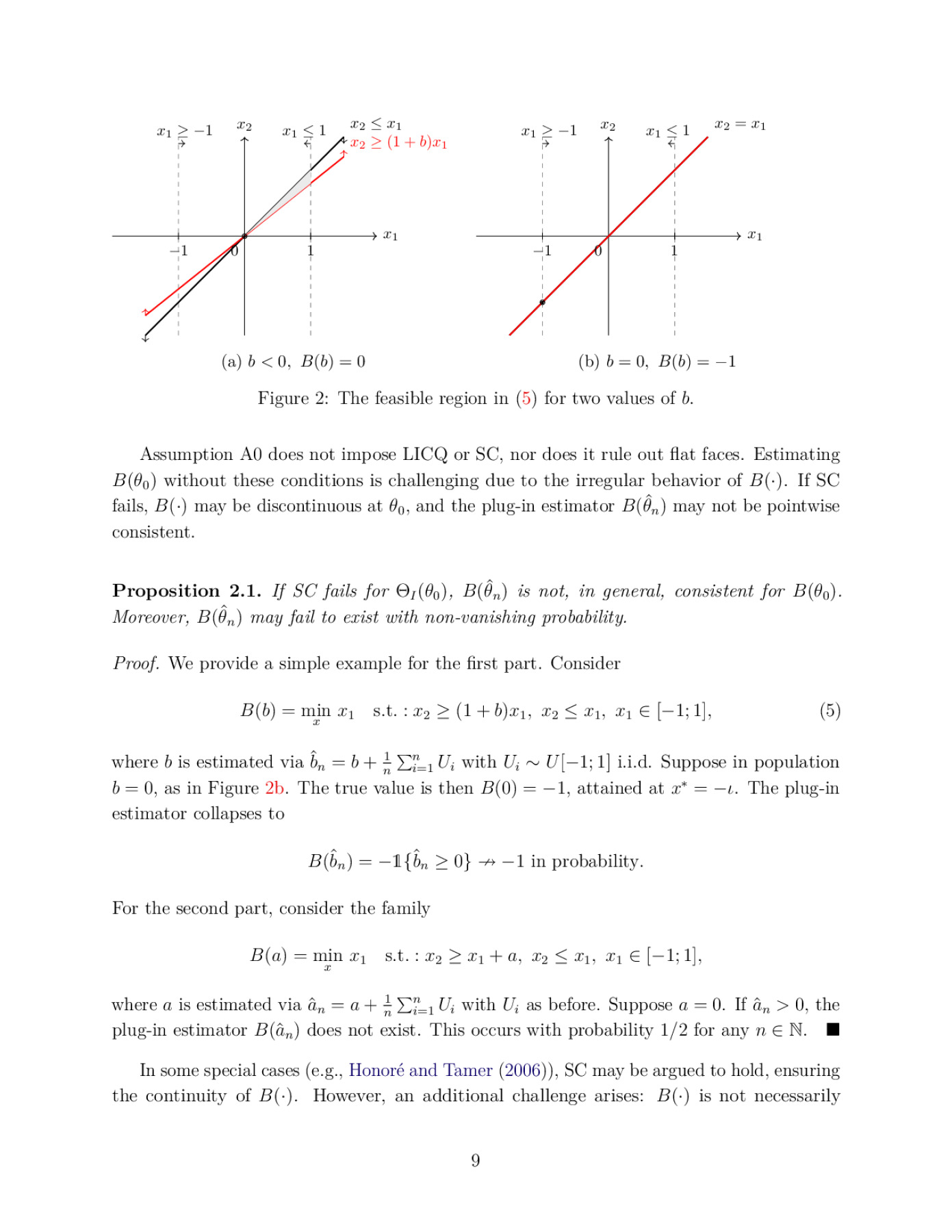
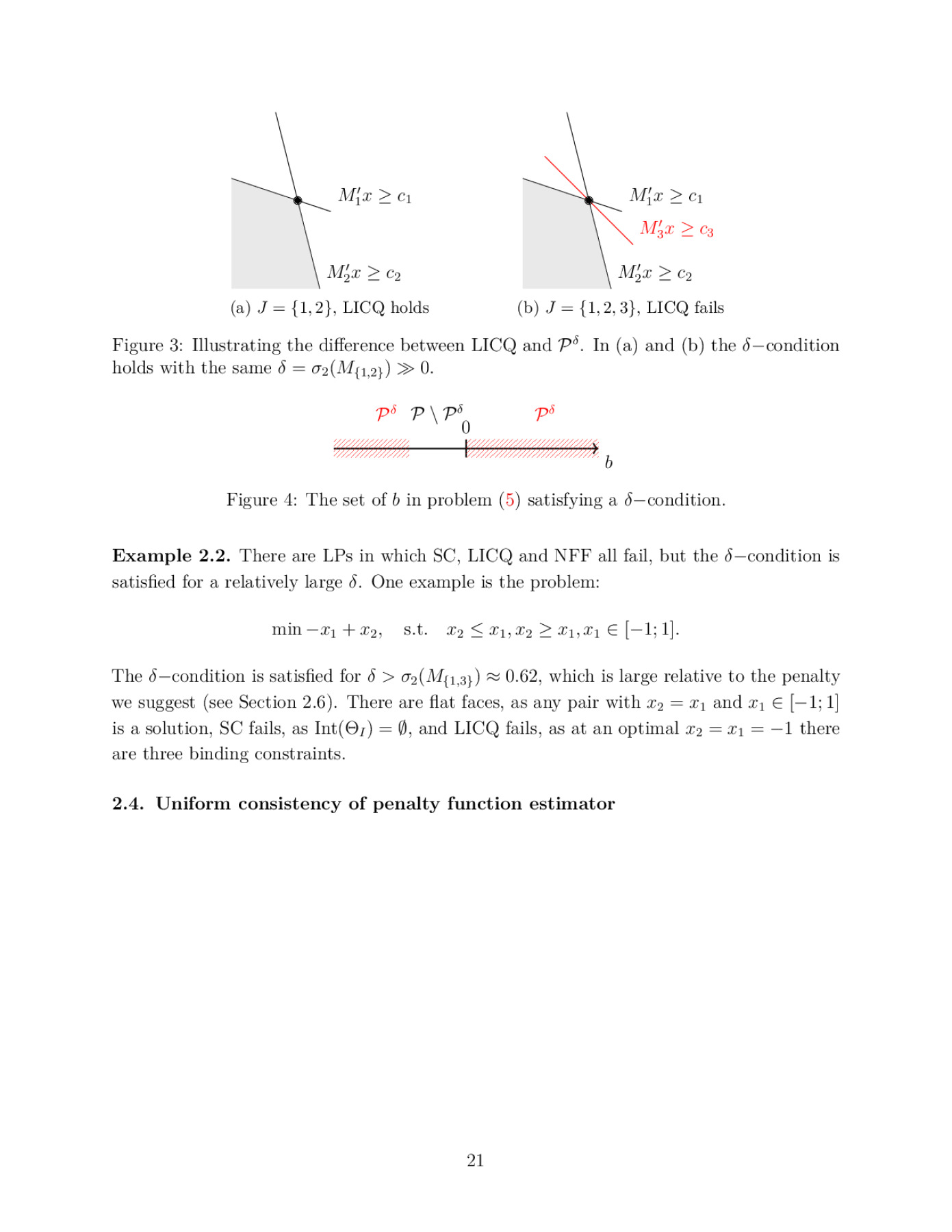
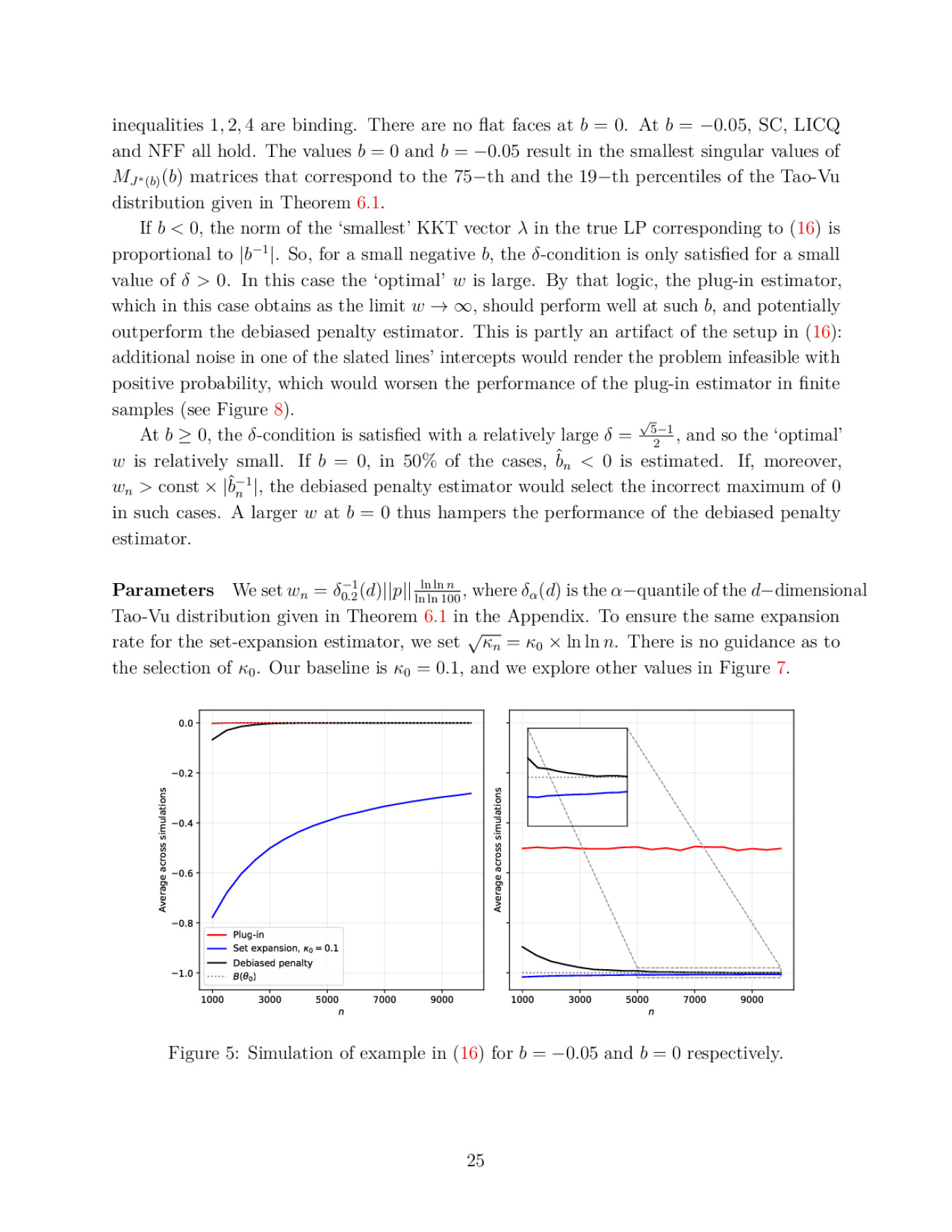
2024 European Winter Meeting, Palma de Majorca, Spain: December, 2024
Linear programming approach to partially identified econometric models
Andrei Voronin
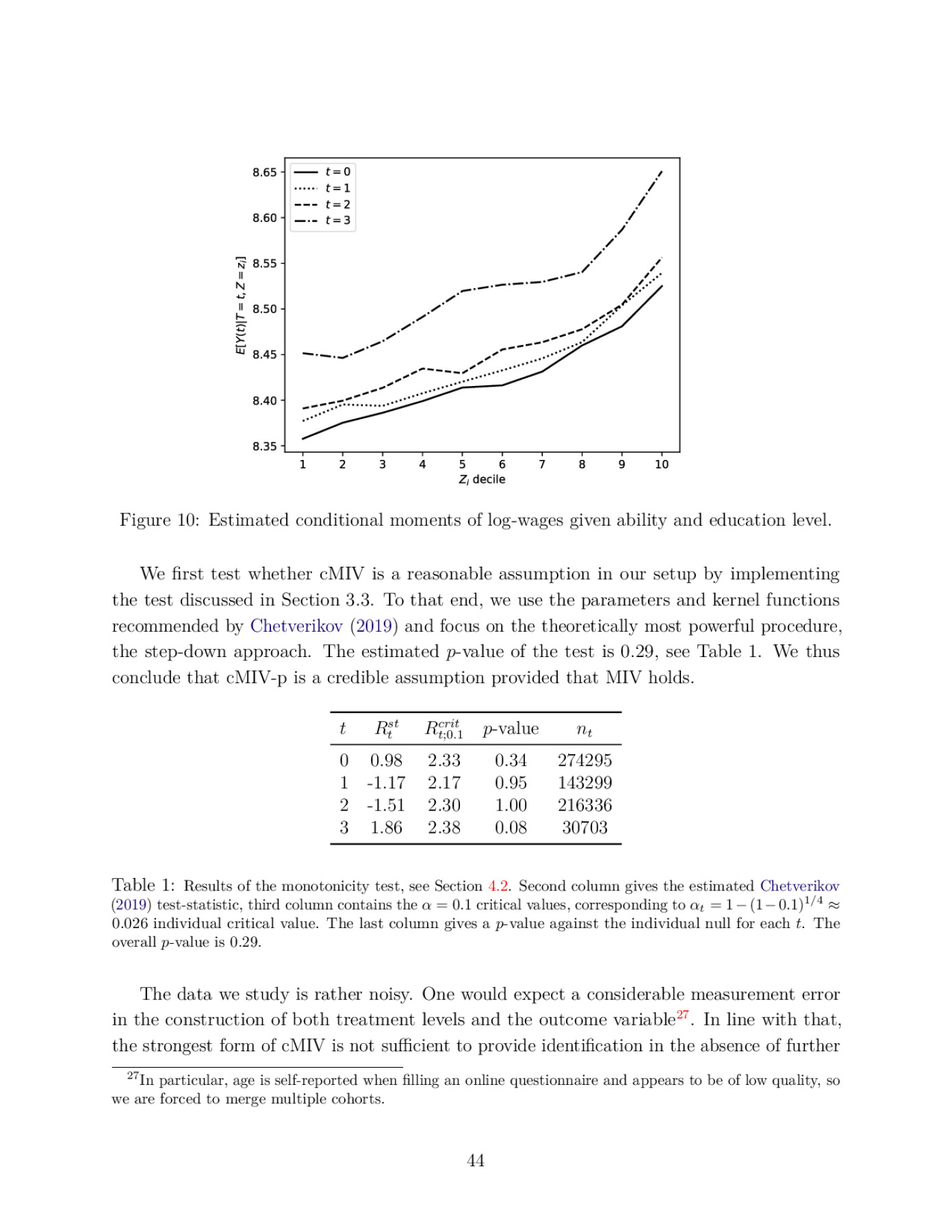
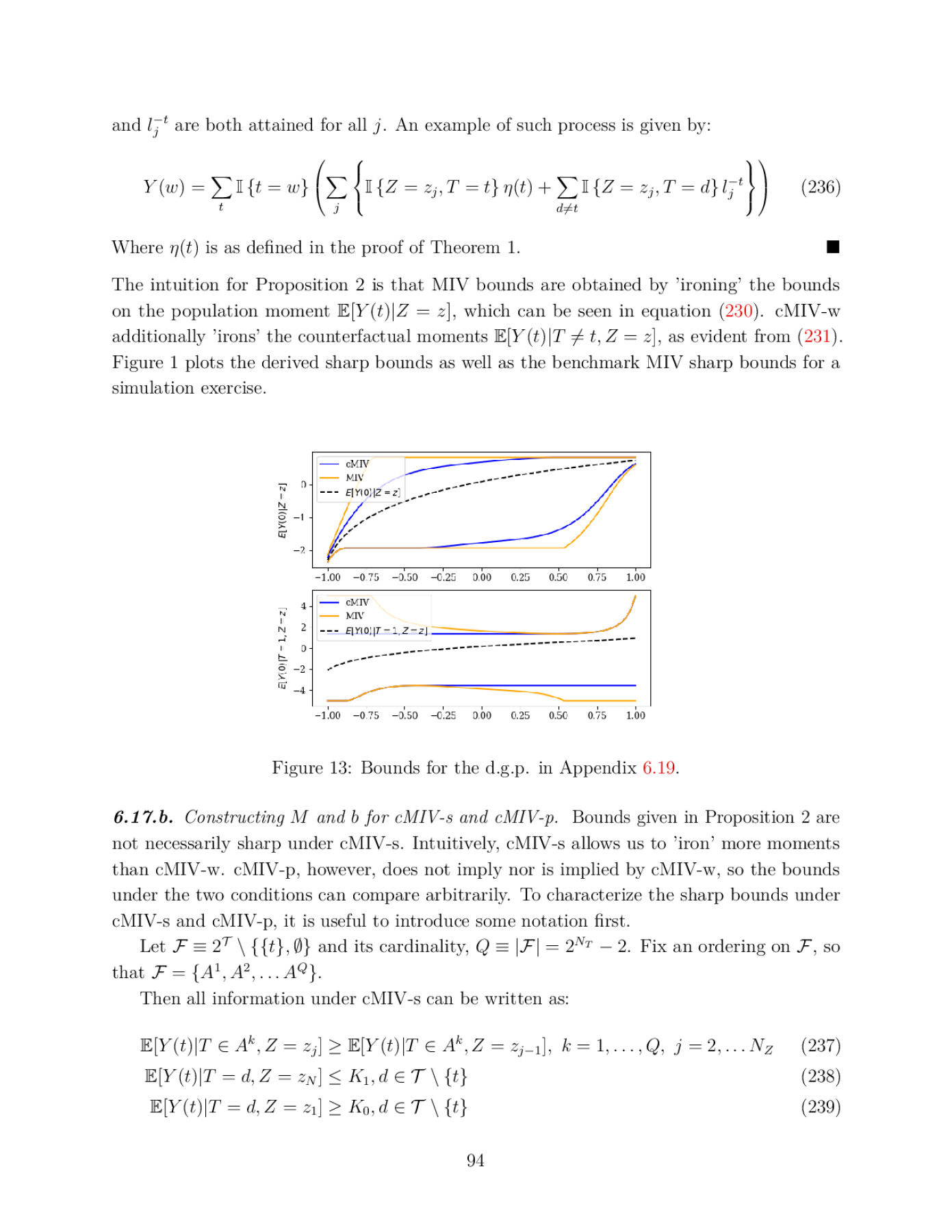
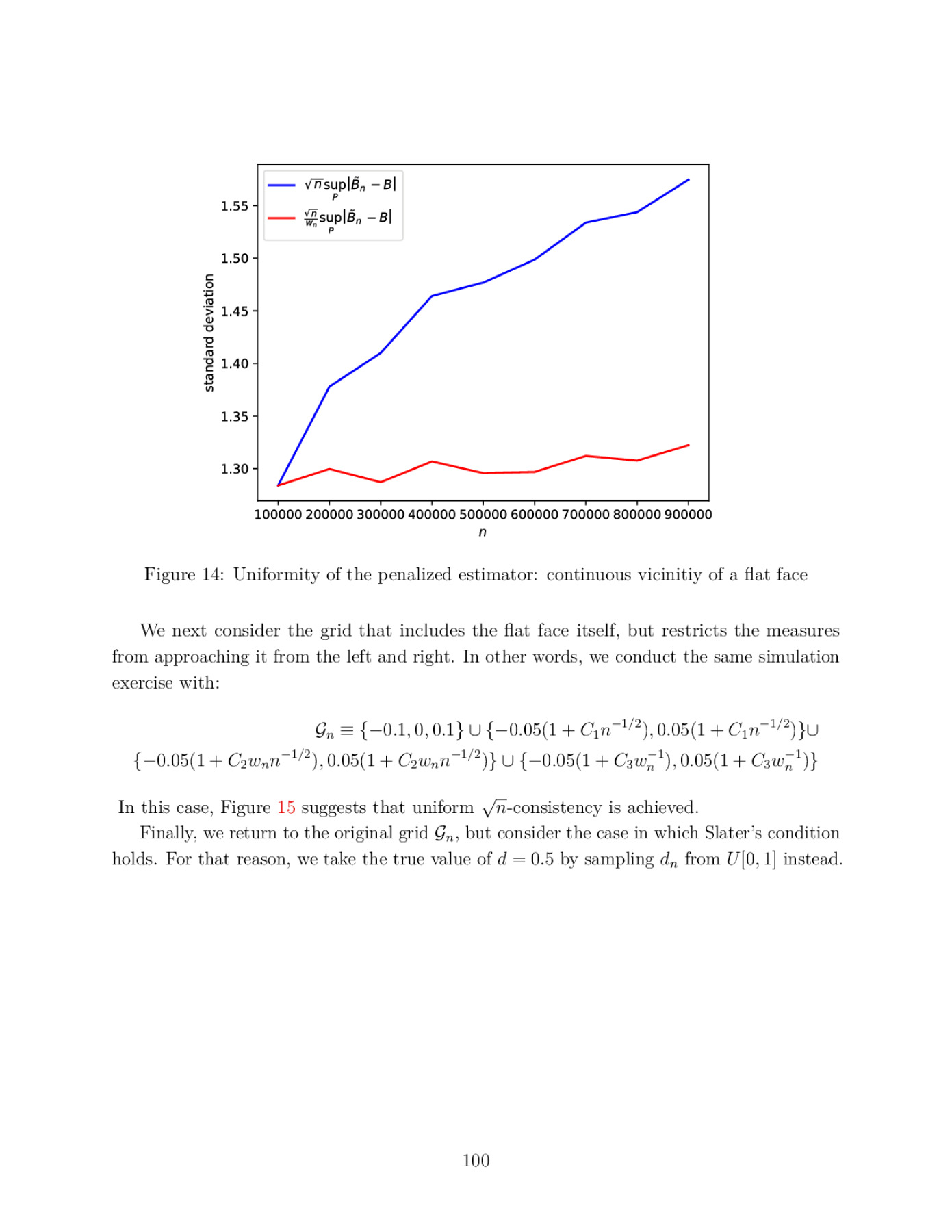
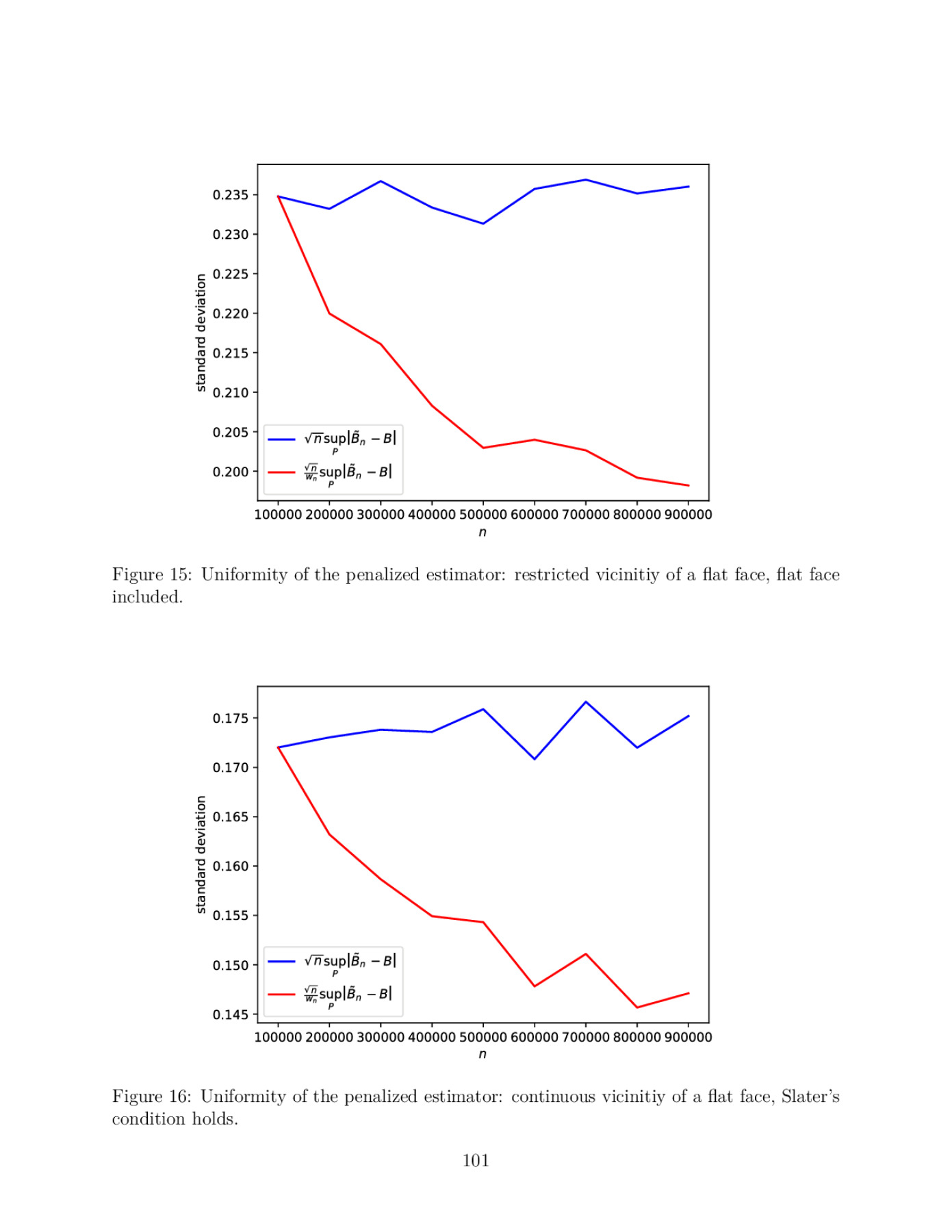
Sharp bounds on partially identified parameters are often given by the values of linear programs (LPs). This paper introduces a novel estimator of the LP value. Unlike existing procedures, our estimator is root-n-consistent whenever the true LP is feasible and finite, and remains valid under point-identification, over-identifying constraints, and solution multiplicity. Turning to uniform properties, we prove that the LP value cannot be uniformly consistently estimated over the unrestricted set of measures. We then show that our estimator achieves uniform consistency under a condition that appears minimal for the existence of any such estimator. We also obtain computationally efficient, asymptotically normal inference with exact asymptotic coverage. To complement our estimation results, we derive LP sharp bounds in a general identification setting. Our approach allows applied work to employ previously intractable conditions. We apply our findings to estimating returns to education. To that end, we propose the conditionally monotone IV assumption (cMIV) that tightens the classical monotone IV (MIV) bounds. We argue that cMIV remains unrestrictive relative to MIV and provide a formal test for it. Under cMIV, university education in Colombia is shown to increase the average wage by at least 5.91%, whereas classical conditions fail to produce an informative bound.
Preview